—

layout: post

mathjax: true

title: (My First Post!) Derivatives Portfolio Compression With Deep Learning (Part One)

In my second post, I propose a radical resolution land inequality in South Africa, drawing mostly from ideas presented in Eric A. Posner and E. Glen Weyl’s book Radical Markets.

Background

The Fight For Economic Freedom

The recent history of South Africa is one of a burgeoning economy and of persistent inequalities. While it is the second largest economy in Africa, it is also the most unequal, as a result of the institutional segregation and discrimination that has plagued the country since 1990. Many compounding factors contribute to the maintenance of this inequality; one of which is the vast inequality in land ownership between blacks and whites. According to a recent land audit, 29.1% of land by value is owned by the government and individuals previously disenfranchised by apartheid, a demographic that makes up 92% of the South African population. Much of this inequality is the result of laws that prohibited black ownership of agricultural lands outside of the reservations where they were forced to live.

Despite constitutionally mandated efforts redistribute the land more evenly amongst racial demographics, progress has been slow, due in part to the government’s policy of “willing-buyer willing-seller”, through which the government would buy land from white land owners for redistribution. The inefficiencies of this mechanism are to be expected, as it is vulnerable to the holdout problem commonly associated with voluntary land markets. Many within the country, particularly the far-left political party EFF (Economic Freedom Fighters), have expressed dissatisfaction with present land redistribution efforts. The EFF recently put forth a motion for a constitutional amendment allowing for “land expropriation without compensation” and it was passed by the nation’s parliament in February. The motion has faced scrutiny from commentators within South Africa and abroad, stating that such a departure from traditional property rights would diminish foreign investment and threaten the nation’s already fragile food security. In the rest of this post, I will discuss a resolution for land inequality that avoids the potentially drastic consequences to expropriation without compensation. The ideas below are covered in more depth here.

The Vickrey Commons Mechanism

The Vickrey Commons is a solution to the infamous holdout problem discussed by Posner and Weyl in “Radical Markets”. The concept stems from a utopian vision by Nobel-Prize winning economist William Vickrey: an ideal economy in which all property is constantly up for auction. In his vision, every capital asset that one could own individually must be mandatorily sold if another individual is willing to pay the asset’s posted value. Vickrey, a pioneer in designing auctions which incentivize participants to bid their true values presented the Vickrey Commons as a way to ensure that no individual sets the sale amount of their asset lower than the amount at which they would actually be willing to part with them. If one were to employ this strategy, he would face significant risk of an opportunistic buyer purchasing the asset a price less than its value to the seller. There is a caveat; if price information is entirely public, that is, if prospective buyers and sellers know the posted sale prices of all items in the economy, there is no incentive to refrain from bidding higher than one’s true value in order to achieve the “market price” of the asset a potential seller holds. This a problem Posner and Weyl solve by introducing another powerful mechanism design from another influential economist.

Benefits of a COST

The “Common Ownership Self-Assessed Tax” complements the Vickery Commons and intends to place a tax on wealth that pays for the social cost of (holding) wealth. Much like the Vickrey Commons, the COST has a simple structure, despite its immense utility. Generally placed on assets with common value, a COST is set somewhere between the turnover rate (which can be thought of as the probability that the holder of an asset loses the asset in a given time interval) and zero. When the tax rate is the same as the turnover rate, an asset holder is incentivized to post her true value as the price of the asset. If she sets it higher, she will pay more in taxes than the expected value of holding the asset. However, like any tax, setting the COST too high would disincentive investments that would increase the value of the asset; as the asset holder does not receive the full return on their investment. The trade-off between the allocative efficiency improvement of the tax combined with the Vickery Commons market ecosystem (the ability for individuals to trade efficiently amongst one another unrestricted by holdout problems) and the investment efficiency (the effects of the tax is illustrated in the figure below, from (Weyl and Zheng 2017)). In the figure $\tau_{eff}$ demarks the COST level that maximizes social welfare, the “sweet spot” between turnover rate and zero (which maximize allocative and investment efficiency respectively).

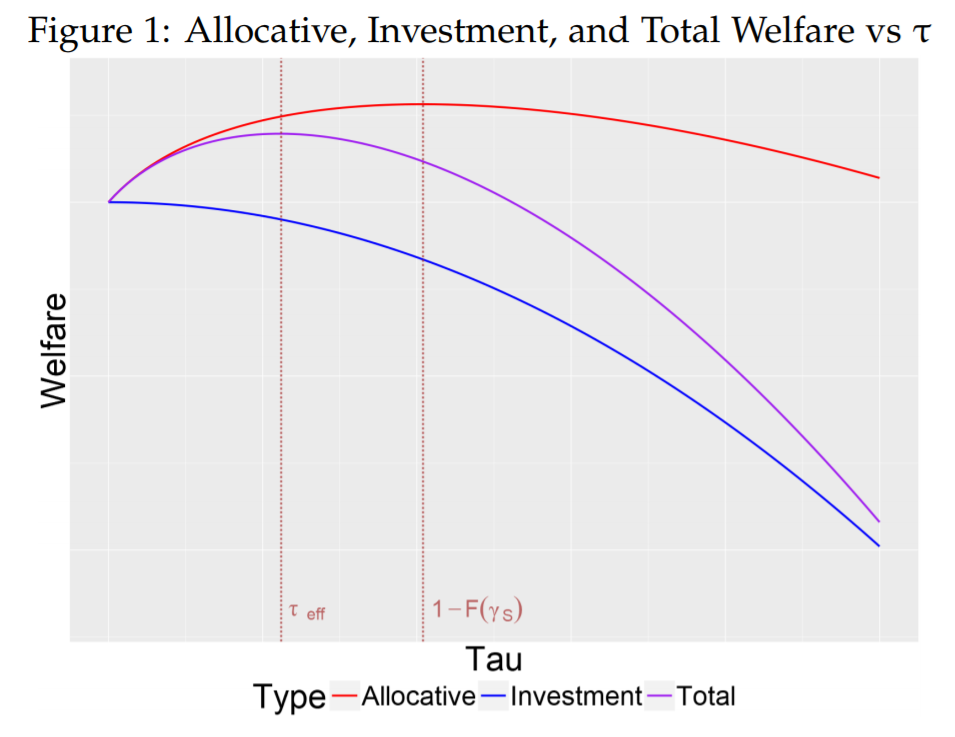
The Vickrey Commons and the COST complement one another to deliver significant welfare gains: The COST disincentivizes individuals from setting their posted price in the Vickrey Commons much higher than its true value (as they will be taxed heftily), while the Vickery Commons disincentivizes people from setting their property value lower than its true value (as it puts them at risk of having their property taken from them without being adequately compensated). In addition, the revenue generated by the COST in a Vickery Commons economy could be significantly greater than revenue generated from property taxes today; taxes would be levied on the true value of assets to individuals, rather than from imperfect appraisals of such assets by adversely incentivized third parties.

Is South Africa ready for a Radical Market?

A Vickery Commons infrastructure with a COST could be a promising way to manage agricultural lands acquired during colonization in South Africa for a number of reasons. Weyl and Posner’s proposal would ensure that the individuals who can generate the most value from the land will receive it, maintaining agricultural productivity, sustaining economic growth driven by foreign investments, and incentivizing service to previously underserved markets (particularly, encouraging more utilization of lands for housing). In addition, if the COST is paid as a dividend to the community, as a universal basic income, or as a way to pay for free higher education, another contentious topic in South African politics, the ill-gotten gains of holding colonized land will be paid back to the South African population. This would provide black South Africans retribution for the socioeconomic inequalities imposed upon them throughout colonization and apartheid. Lastly, the mechanics of the COST align strongly with rhetoric and actions concerning land reform in the recent past; it seems to echo the wishes of EFF leader Julius Malema and of black South Africans who have made claims on land which they previously inhabited.

Welfare Gains From The COST

In Radical Markets: Uprooting Capitalism and Democracy, Glen Weyl and Eric Posner estimate the egalitarian benefit of applying a COST to all capital in the United States. Using a similar methodology, one can estimate the benefits a COST on South African agricultural commercial lands. Currently, the total value of commercial agricultural land in South Africa is $18 billion. At the rate of roughly 7% annually that is conjectured to be near-optimal (the $\tau_{eff}$ displayed in Figure 1) levying an additional COST tax on the value of land would leave the South African people with 1.26 billion dollars of additional revenue which could be set aside to completely fund progressive initiatives further diminishing inequality within the nation (free higher education for ambitious low-income South Africans, universal basic income to give the labor force time to reskill for the new economy). While the lower bound of expected tax revenue would be modest, Weyl and Posner project that the asking price of capital in a radical market economy would triple the total value of all land, (as individuals’ true value of capital is higher than the market value in a market in which sales are voluntary) which would in turn triple tax revenue.

Malema’s Own Words

Julius Malema is a controversial figure in South African politics, and is perceived to be quite the radical himself. However, when it comes to discussion of what he intends to do with the land once it is expropriated, his own words suggest that he is quite open to use of the land taking place in a market ecosystem. He has emphasized “people say when the land is in the hands of the state‚ there will not be investors. It is a myth. It is wrong.” He cites facilities owned by the state such as uShaka Marine World, a marine theme park, as examples of state-owned land that has not sacrificed all investment efficiency, and stresses that an effective solution to the land disparity will not involve a departure from private land investment. In addition, he has also commented that the main targets of expropriation should be land that is inappropriately utilized due to the high social cost of holding wealth. In March of 2018, he stated that farmers should continue to work their land “uninterrupted”, but that those parts that are lying idle must be “redistributed by the state”. He elaborates that the idling parts of farms should be relocated to those who will use it for production, signaling that he wishes to use land expropriation to drastically improve allocative efficiency, an ends to which William Vickery would strongly agree.

While it is clear that the ends of Julius Malema’s land expropriation plan mirror the ends of a Radical Market infrastructure like the Vickery Commons, it is not clear that Malema, or the EFF are the slightest bit flexible on the means. Malema strongly believes that land is a public good, and thus, the government should be in charge of determining who is best equipped to use it. On the other hand, the Vickery Commons, proposed by Posner and Weyl suggests that the public nature of land does not imply that its ownership must be monopolized by the state, but rather, that it should be decentralized as much as possible with dividends on its profits being paid back to support equal economic opportunity for all permanent residents. This divergence is stark, but it would definitely be worthwhile explore which methodology would better achieve their shared aim of significant welfare improvement. A cursory glance, within the context of recent history, suggests the free-market solution to this historically racial holdout problem more powerfully improves efficiency than a solution implemented, enforced, and micro-managed, by a tragically imperfect state.

Next Steps

In future blog posts, I would be interesting in exploring the feasibility of a using a COST for redistributing land wealth amongst South Africans, and as an alternative to land expropriation without compensation. I would also like to explore whether COST is in alignment with the South African constitution, and more closely estimate the exact welfare gains that could be achieved using the mechanism. Stay tuned!

For my first post, I’d like to focus on a very interesting intersection between financial economics and computer science I have been working on for the past semester while completing an undergraduate research project. This particular juncture is derivatives portfolio compression, a particularily important activity for financial firms looking to decrease their notional liabilities (due to recent regulatory obligations, a decrease in liabilities results in an increase in the flexibility institutions have to invest in capital.)

Portfolio compression is multilateral netting operation completed after a set of trades, which reduces counterparty risk (gross exposures between financial institutions) and maintains market risk (net exposures). Portfolio compression is unique from other netting operations because it reduces participant’s gross positions by tearing up redundant obiligations. In addition, portfolio compression can exploit multilateral netting opportunities without the participation of a Central Clearing Counterparty (CCP). Below is a stylized example of portfolio compression on a market consisting of four financial institutions:

My research this past semester has consisted creating an Open AI Gym environment that models this problem for the training of a reinforcement learning agent. The goal of this agent would be to derive an ofor compressing a set of derivatives contracts between groups of banks. Given the recent resurgence of financial regulation incentivizing actors within the financial sector to minimize their excess derivative contract notional, devising an artificial intellegence system to automatically minimize this excess over time is certainly a worthwhile endevour.

Problem Statement

Perhaps I should more concretely define the problem I intend to solve, before diving deeper into the OpenAI Gym I designed to acheive a solution.

First, we must define the following notation, a derivatives market can be modelled as consistenting the following elements:

1. A set of banks $B$ comprised of banks $(b_0,b_1,\dots b_n)$.
2. A set of timesteps $T = (0,1,2,3,4,5,\dots,n)$; each timestep $t \in T$ represents a week during which derivatives trading occurs.
3. A set of edges for every timestep $t$ that comprise a directed graph $G_t$, $E_t = (e_{t0},e_{t1}, \dots e_{tn})$; each edge $e_{ti} =(b_j,b_k)$ is of weight $w_t$, which represents an debt owed of $w$ million euros from bank $b_j$ to bank $b_k$ at timestep $t$.
4. An “arrival” of an edge is defined as one of two events:
   1. The origination of an edge $e_ti =(b_j,b_k)$ that did not exist in prior timesteps.
   2. The increase of the weight $w$ of an edge $e_ti$ that had existed in prior timesteps.
5. The total notional of a derivatives contract graph $G_t$ is equivalent to:

Where $w_t(b_i,b_j)$ is a function that returns the weight $w$ of the edge defined as a derivative contract relationship between bank $i$ and bank $j$ at timestep $t$.

Minimizing total notional at a given timestep $t$ is a solved problem, a paper that discusses the network simplex solution and how it effects a given derivatives contract network $G_t$ can be found here.

The precise problem that a intend to allow a reinforcement agent to learn how to solve is this:

If edges (derivative contracts) that arrive between banks due to a pattern determined by banks within a given financial system, can an agent to learn minimize notional excess over all periods? This can be formalized as solving for:

Where $w_t(b_i,b_j)$ is a function that returns the weight $w_t$ of the edge defined as a derivative contract relationship between bank $i$ and bank $j$ at timestep $t$.

Reinforcement Learning Problem

The corresponding reinforcement learning problem is very similar to the problem statement above, but with a few simplifications. They are outlined below:

1. We will only be attempting to solve for the minimum amongst the top 10 most connected nodes, based on initial analysis, one can see that there are very few very connected nodes, so this is a fair simplification for the more general problem. A histogram is shown below:

1. For the early stages of this project, we will only aim to keep total notional below a certain percentage of what I define as counterfactual total notional, which is the total notional that would at time $t$ be observed given no action on all derivatives contract graphs $G_i$ for all $0 \geq i < t$, as of right now, this percentage of notional is set at 60%

Reward Structure

The reward structure of this problem is quite simple, our agent will recieve a reward of $-1$ for every time step it spends with total notional above the given threshold and positive 1 otherwise. Below is the “_get_reward” function in our OpenAi Gym environment.

def _get_reward(self):
        """Reward is given for each timestep below the is_compressed threshold."""
        if self.is_compressed:
            return 1
        else:
            return -1

Action Structure

As previously mentioned, minimizing the total notional amongst a set of banks $B$ and their respective edges $E$ while maintaining the amount owed from each bank to every other is a solved problem. It can be solved using the following linear programming problem:

Where $\hat{u}$ is a vector of all 1’s, $e’$ is the set of edges that would minimize total notional, $Q$ is an incidence matrix of our derivatives contract graph $G$ and $v$ is a vector representation of the total degree of each bank (which represents underlying value on each banks balance sheet).

To figure out which cycles can be compressed in order achieve the minimum notional solution to the above linear programming problem, one could simply solve the problem, and subtract the solution of the problem from the original adjacency matrix. I denote this as the “critical adjacency matrix”. It is composed entirely of “critical cycles” or non-overlapping cycles that must be removed in order to completely conservatively compress a credit derivatives network graph. The actions that our agent can take are comprised of removing the first $i$ critical cycles, where $i$ is defined by the agent. The critical cycles are ordered by the decrease in notional excess, so removing the first $i$ critical cycles removes the $i$ critical cycles contributing most to unneccesarily high gross notional. If $n$ is the total number of critical cycles, action $n$ of our agent corresponds to subtracting all $n$ critical cycles from the current adjacency matrix (the adjacency matrix upon which the agent acts). Below is an example of a stylized derivatives contract market, its corresponding compressed market, and its corresponding “critical set”. The cycles of this graph are the critical cycles of the derivatives contract network.

Observation Structure

State Observations

THe observation structure of my agent is comprised of three components. The agent observes the state it exists in (the current derivatives contract market $G_t$), the actions it can take, and the reward it has recieved from its previous actions. After it makes a specific action, the agent sees an adjacency matrix repesenting derivatives contracts that have originated up to timestep $t$ between the top $m$ banks with the highest node centrality. As an adjacency matrix is a very noisy way to view and try to discern patterns within a derivatives contract graph, I have looked quite seriously into using the first $k$ singular values of the adjacency matrix to derive a rank $k$ representation of the adjacency matrix.

Action Observations

In addition, the agent observes the critical cycles of the adjacency matrix representing the culmination of derivatives contracts up to timestep $t$, these critical cycles are calculated by utilizing a conservative compression linear programming algorithm to find the graph that minimizes the notional excess of our derivatives contract graph. I then subtract this graph from the “current adjacency matrix” as described in “State Observations”. The cycles of this graph consist entirely of “critical cycles” or cycles that should be removed in order to miniminze excess notional in the derivatives contract graph. Given $n$ critical cycles, our agent can choose between action $ 0 < i \leq n$ where choosing action $i$ runs the following algorithm, as described in D’Errico and Roukny, for the first $i$ critical cycles (The critical cycles are ordered by the excess notional removed when they are compressed):

def compress_critical_cycle(ccycle,adj_matrix):
    path = ccycle['cycle']
    path_edges = [(path[i-1],path[i]) for i in range(1,len(path))]
    min_edge = min([adj_matrix[edge] for edge in path_edges])
    for edge in path_edges:
        adj_matrix[edge] = adj_matrix[edge] - min_edge
    return adj_matrix

Reward Observation

THh last observation to touch on is the observation that allows the agent to best discern how close it is to an optimal reward. Every timestep, our agent recieved information stating the current excess_percent. Which is the percent of counterfactual notional that is currently achieved by the current adjacency matrix. This is the same metric that will decide if an agent will recieve a reward of positive or negative 1 during a given timestep.

_get_state logic is displayed below:

    def _get_state(self):
        """Get the observation."""
        self.counterfactual_adj_matrix = self.counterfactual_adj_matrix + self.week_adj_matrices[self.curr_date]
        self.curr_adj_matrix = self.curr_adj_matrix + self.week_adj_matrices[self.curr_date]
        excess_percent = np.sum(self.curr_adj_matrix)/np.sum(self.counterfactual_adj_matrix)
        compress_res = compress_data(self.curr_adj_matrix)
        critical_matrix = compress_res["critical_matrix"]
        compressed_matrix = self.curr_adj_matrix - critical_matrix
        self.ccycles = critical_list_from_matrix(critical_matrix)
        return dict({"curr_adj_matrix":normalize_matrix(self.curr_adj_matrix),
                    "compressed_matrix":normalize_matrix(compressed_matrix),
                    "excess_percent":excess_percent})

Results

Unfortunately, due to the time constraints of the semester, I was unable to build a deep learning agent to train within in the OpenAI Gym I intended to build. However, I was able to build the gym environment and to test various policies on it. For these tests, I used the 10 most connected banks and I used the timesteps of the 57 weeks from January 5th, 1999 to Febuary 8th, 2000. I tested 3 policies for 100 episodes:

1. A policy in which the agent compresses all critical cycles left in the derivatives market’s graph. At every timestep, this policy calculates the critical cycles of the graph and compresses all of them.
2. A policy in which the agent compresses 500 critical cycles left in the derivatives market’s graph. At every timestep, this policy calculates the critical cycles of the graph and compresses all of them.
3. A policy in which the agent compresses a random number of cycles.

Below are the eliminate notional at each time step by each policy. The minimum notional achieved by the random policy uses an average of 100 random polices. The red line, denoted “minimum notional” calculated as the the minimum notional achieved if at the last time step, the algorithm described in Roukny and D’Errico is run. This is the minimum possible excess percent utilizing conservative compression. A compression policy can be evaluated by its distance towards this metric, which for this time interval, and this number of banks is about 44%.

While it would be intuitive that compressing all cycles at every timestep decreases notional significantly, the figure above shows that this is not the case. In fact, there is a great deal of room between the minimum notional (44%) and the resulting notional from the three policies analyzed, which seem to have equivalent success. This “optimization gap” is nontrivial, as it leaves about 13 billion euros uncompressed in the european credit derivatives market. The lower level achieved by compressing only 500 cycles each timestep seems to suggest the presence of a “happy medium” between compressing all cycles and compressing no cycles that yields lower excess notional at the end of each episode (one round of compressing at every time step). This “happy medium” could likely be found by a reinforcement learning agent.

It is also noteworthy that there is a great deal of variation in results amongst the random agent’s 100 episodes. Below is a plot denoting the random agents average performance, its maximum performance, and its minimum performance.

Next Steps

1. Build a deep learning agent trained with my model, as of right now the cross entropy agent from the OpenAI Gym package that I am using has quite poor performance; I made this gym enviroment to test architectures with stronger pattern recognition abilities, and I certainly would like to test my environment on such architectures.

2. I have been playing quite a bit with the idea of sending the reinforcement learning agent information about only portions of the singular value decompisition of the “current state adjacency matrix” (such as its SVD). This would help accentuate patterns within the adjacency matrix amongst banks with very distinct trading patterns. Once I am able to begin to work more seriously on using a deep learning architecture for policy discovery this will definitly be the first mutation of the very noisy adjacency matrix that I will try.

Codebase

The Open AI Gym I built, and the random agents I used to test it is all public here on my github.